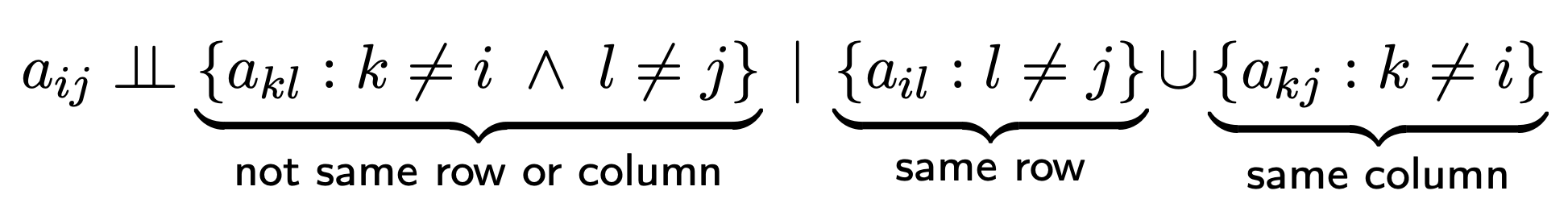
Recommender Systems

We analyze patterns of interest in items (products, movies) and provide personalized recommendations for users.

Collaborative Filtering

We want to exploit collective data from many users and generalize across users, and possibly across items.
Example applications are Amazon, Netflix, online advertising, etc.

Netflix Data

Input: user-item preferences stored in a matrix

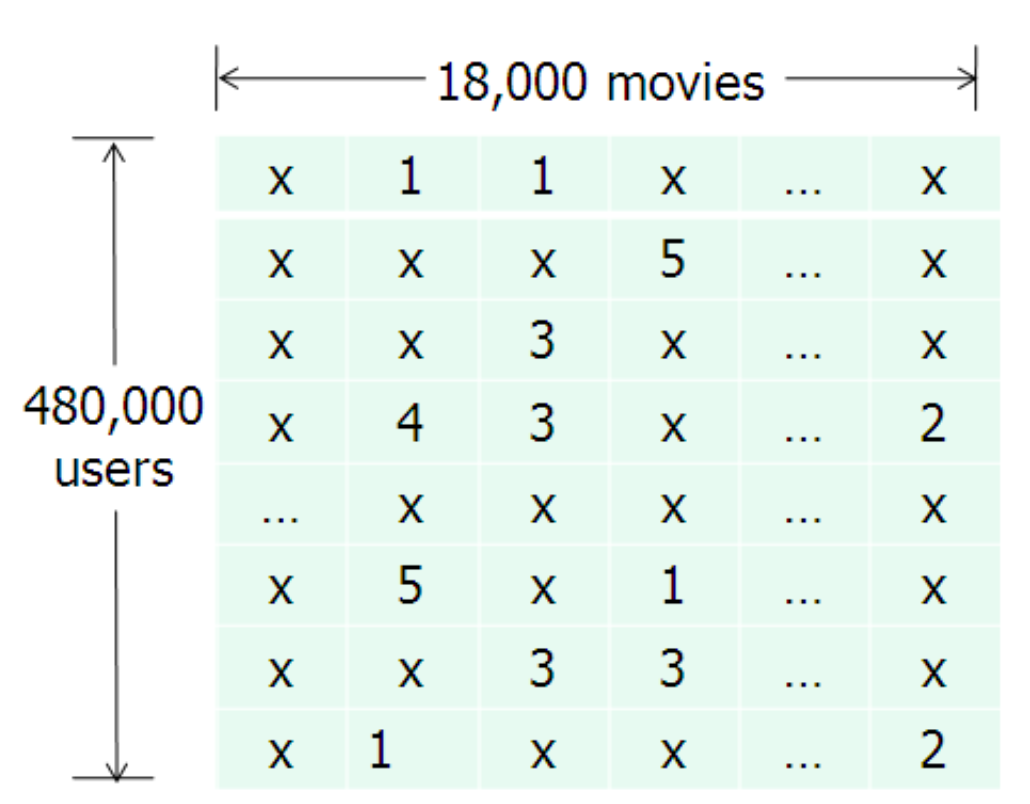
Sparseness level can be very low, 1% and less

Formal definition:

$n$ number of users (rows)
$m$ number of items (columns)
$\mathrm{\Omega }$ observation matrix, where $w_{ij}=1$ iff $a_{ij}$ is observed

Preprocessing / Normalization

Centering

Mean rating per user/item

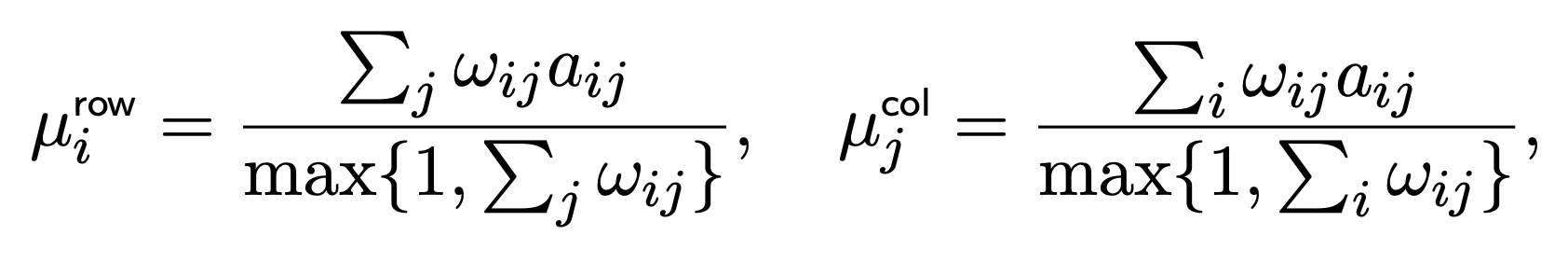
This lets us center the data:

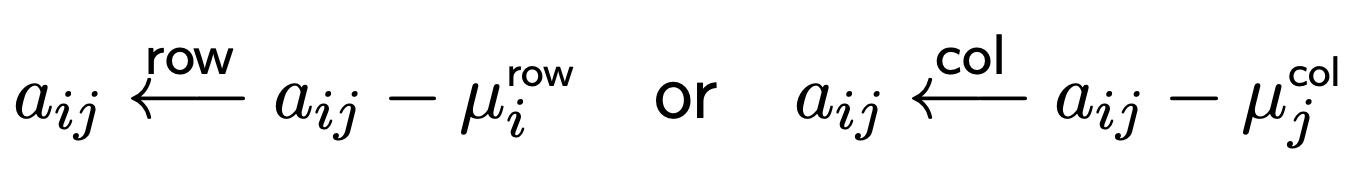
Variance Normalization

$\mu =\mathbf{\text{E}}[X]$
${\sigma }^2=\mathbf{\text{Var}}[X]$
Then the noramlized scores or z-scores are:
$Z=\frac{X-\mu }{\sigma }$

Convexity Definition

If $f$ is differentiable, convexity is equivalent to the condition:
$f(x)\ge f(y)+\mathrm{\nabla }f(y)(x-y),\mathrm{\forall }x,y\in R$
if $f$ is twice differentiable, convexity on a convex domain $R$ is equivalent to the condition:
${\mathrm{\nabla }}^{2}f(x)⪰\mathbf{0},\mathrm{\forall }x\in \mathbf{Int}(R)$

Our scalar problem is non-convex (exception: $a=0$), as there is a saddle point at the origin.

Gradients

Vector / Matrix notation
$\nabla_u l = Rv, \quad \nabla_vl = R^Tu, \quad R := (uv^T - A) $

Hessian Map

$ \nabla^2 l(u,v) = \left( \begin{matrix}
||v||^2 1_{n \times n} & 2uv^T - A\
(2uv^T - A)^T & ||u||^2 1_{m \times m}
\end{matrix} \right)$Attheorigin:$\nabla^2 l(0,0) = \left( \begin{matrix}
0 & -A\
-A^T & 0
\end{matrix} \right)$
This is scalar to the mulitdimensional case. The hessian at zero is not positive-semi-definit , unless $A$ is nilpotent (has all zero eigenvalues).

This problem is non-convex for all dimensions $m,n\ge 1$

Gradient Flow

Assume $u=v$, balanced initialization and they evolve identically.
We look at $x=uv=u^2$:
$\begin{array}{rl}\frac{du}{dt}& =-v(uv-a)\\ \frac{dx}{dt}& =\frac{d{u}^2}{dt}=-2uv(uv-a)=-2x(x-a)\end{array}$
This ODE can be solved, yields:
$x(t)=\frac{a{e}^{2at}}{e^{2at}-1+(a/c)}=a+\frac{ac-a^2}{c{e}^{2at}+a-c}$

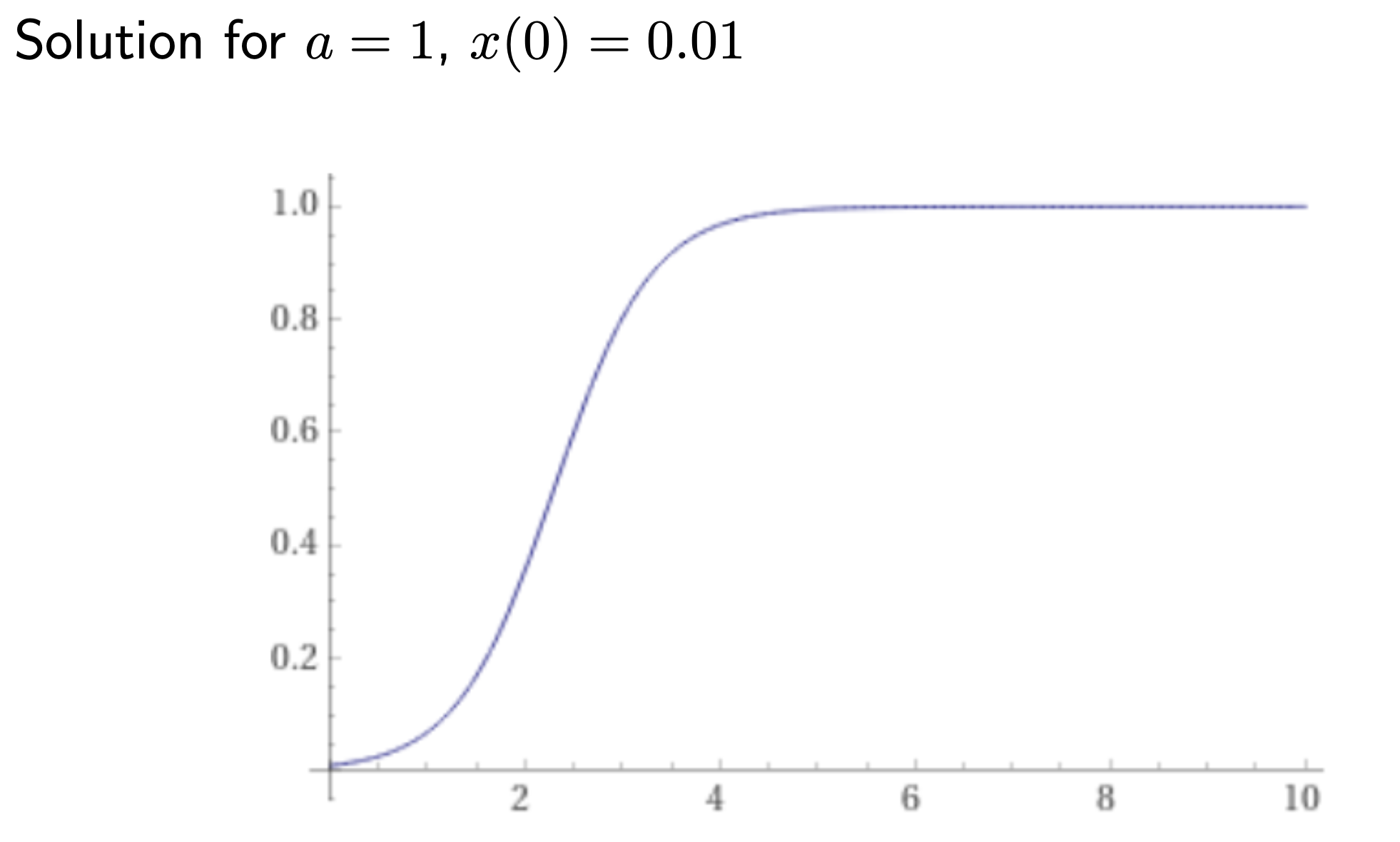
Fully observed Rank 1 Model

Useful identiy:
$||R|{|}_F^2=\text{tr}(R^{T}R)$
We can then rewrite the objective:
$l(u,v)=\frac{1}{2}||A-u{v}^T|{|}_F^2$

Optimality Conditions

Directionality of $u,v$ is purely determined by the last term:
$(u,v)\to max\{u^{T}Av\},\text{s.t.}||u||=||v||=1$
This can be solved with Lagrange multipliers:
$\mathcal{L}=u^{T}Av-\lambda u\cdot u-\mu v\cdot v$
First order optimality condition:
${\mathrm{\nabla }}_u\mathcal{L}=Av-2\lambda u\stackrel{!}{=}0\Rightarrow u=\frac{Av}{||Av||}$

Eigenvector Equations

By putting both optimality conditions together we get the eigenvector equations:
$u\propto (A{A}^T)u,v\propto (A^{T}A)v$
$u$ should be proportional to the principal eigenvector of $A{A}^T$
$v$ should be proportional to the principal eigenvector of $A^{T}A$
Power iterations can be used for computation.

The generalization of this results in the Singular Value Decomposition