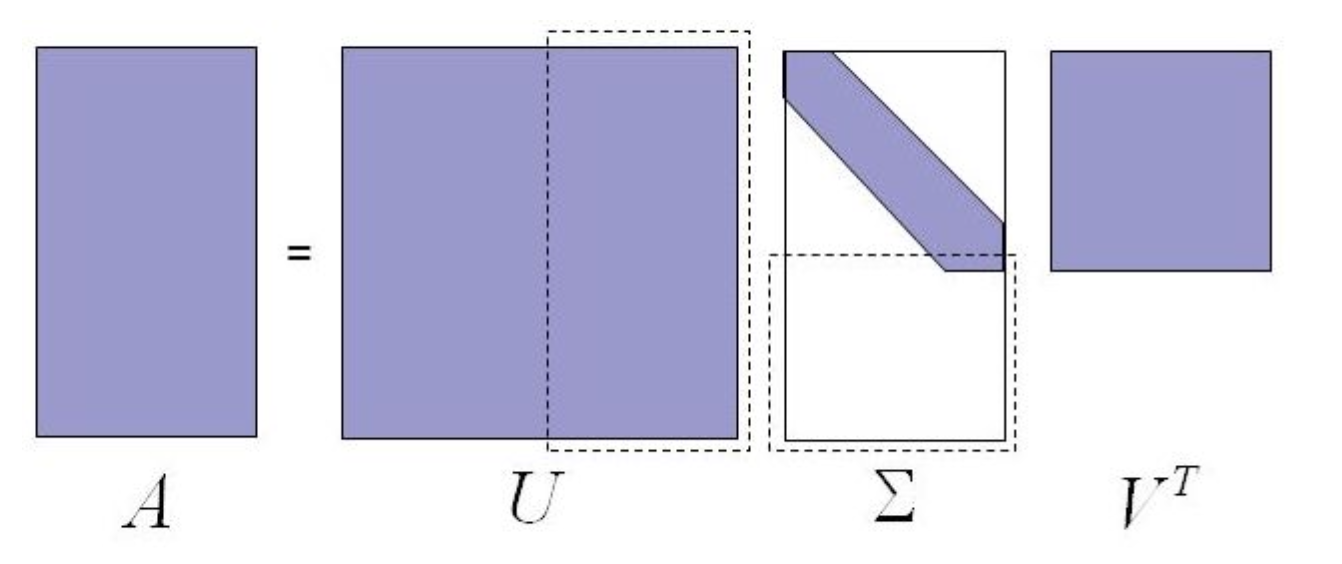
Singular Value Decomposition

SVD Theorem

For each matrix $A\in {\mathbb{R}}^{n\times m}$, there exist orthogonal matrixes $U\in {\mathbb{R}}^{\mathbb{n}\times \mathbb{n}}$ and $V\in {\mathbb{R}}^{m\times m}$ such tat $A$ can be expressed as:

• The set of singular values is unique
• Left/right singular vectors (columns or $U$ and $V$) can have arbitrary sign

Computation Complexity

SVD and Frobenius norm

Let the SVD of $A\in {\mathbb{R}}^{n\times m}$ be given by $A)U\mathrm{\Sigma }{V}^T$, then:

SVD and Spectral norm

Let the SVD of $A\in {\mathbb{R}}^{n\times m}$ be given by $A)U\mathrm{\Sigma }{V}^T$, then:

Reduced SVD

One can often prune columns of $U$ or $V$ corresponding to zero elements in $\mathrm{\Sigma }$ (or zero-padded columns/rows)